2. Folytonos Folyamatok MODELLEzése

2.1 Irányított Folytonos folyamatok

Már láttuk, hogy ha egy rendszer (folyamat) állapotát leíró az x(t) vektorfüggvény (adathalmaz) időben folytonos, akkor az illető rendszert (vagy modelljét) időben folytonosnak nevezzük. Ha az állapotot leíró x(t) vektorfüggvény (adathalmaz) csak bizonyos (ún. mintavételezési) időpontokban ismert, úgy a rendszert (illetve annak modelljét) időben diszkrétnek (mintavételesnek) nevezik. Az időben diszkrét folyamatokat és főleg azok modelljeit általában a folytonos folyamatokhoz soroljuk, mert gyakran csak a folytonos folyamatok számítógépes megközelítése (szimuláció, digitális irányítás, identifikáció, stb) miatt dolgozunk mintavételes modellekkel.

A folytonos folyamatok modellezésének elsődleges célja az illető folyamat műszaki, gazdasági, társadalmi céloknak megfelelő önműködő irányítása. A továbbiakban elsősorban az ipari, termelési, gyártási folyamatokra és azok irányítására gondolunk.

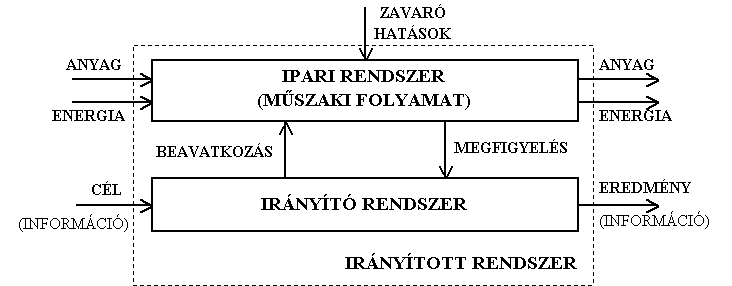
Az irányítás egy olyan tevékenység, amely egy (műszaki) folyamatot elindít, fenntart, megváltoztat vagy leállít, bizonyos kitűzött céloknak megfelelően. Az önműködő irányítás műszaki megvalósítója az irányító rendszer (berendezés), amely az (emberi) irányítási tevékenység funkcióit hivatott kiváltani. Az irányítás 3 fő funkciója:

- az információszerzés (megfigyelés)

- az információfeldolgozás és a döntéshozatal

- a beavatkozás

Az ipari rendszer műszaki folyamatai ennek bemeneteit, anyagot (nyersanyagot, félkész terméket, stb) és energiát, alakítják át. Az energia általában külső forrású, de maga az ipari folyamatban az anyag átalakulása során is keletkezhet A rendszer kimenetén az átalakítás eredménye szintén anyag és energia formájában jelentkezik. Az eredmény a hasznos termék (késztermék, hasznosítható melléktermék, energia), de rendszerint hulladék (nem hasznosítható melléktermék, energia) is keletkezik.

A műszaki folyamatokat a valóságban elkerülhetetlen külső és belső zavaró hatások érik. Ezek a zavarások is a valószínűbb, rendezetlenebb, általában a nem kívánatos irányba terelik a rendszer állapotát. Ezért a kimeneten a kívánt eredményt csak külső beavatkozással, a folyamatok célszerű irányításával érhetjük el.

A beavatkozás a folyamat előre megtervezett kívánt (elvárt) állapota és annak tényleges (megfigyelt) állapota összehasonlításával ésszerű döntések alapján történik. A beavatkozás általában a folyamatban lezajló anyag- és energiacserékbe kívülről a lehető leghatékonyabb helyen történik (vagy kell megtörténjen). Mindez az illető folyamat fejlődésében, (át)alakulásában, állapotjelzőinek idõbeli értékváltozásaiban nyilvánul meg. Az irányított rendszert tehát lehetőleg mindig dinamikus rendszerként kell kezeljük (modellezzük).

Az irányítási funkcióik megvalósításában az információ (és nem az anyag/energia) játszik szerepet. Az irányító rendszer az irányítás céljára vonatkozó információt a rendszeren kívülrõl, rendszerint ember-gép kommunikáció (ilyen lehet pl. egy program) illetve megfelelő műszerezés (érzékelő szervek) segítségével kapja. Ennek az információnak a feldolgozása illetve a döntéshozatal megvalósítása a műszaki folyamatnak (illetve modelljének) ismerete nélkül gyakorlatilag lehetetlen. Ezért a modell-alapú irányítás elnevezést és gyakorlatot gyakran szoktuk használni.

A folytonos (műszaki) folyamatok irányításához szükséges modellezésben általában a funkcionális modellezés módszereit alkalmazzák. Tudjuk, hogy maga ez az eljárás alulról felfelé építkezik. Ezért előbb a rendszert funkcionális részegységekre (alrendszerekre) kell lebontani, majd a rendszermodellt az egymással kapcsolatban lévő funkcionális modulok (szervek, tagok) segítségével kell felépíteni.

A szerv egy irányítási funkciót megvalósító szerkezeti egység (ilyen az érzékelő szerv, a beavatkozó szerv, a végrehajtó szerv, a vezérlő szerv, a szabályozó szerv).

A tag az irányítástechnikai szempontból tovább nem bontható, illetve önálló funkciót megvalósító szerkezeti egység. A tagok jelentik a funkcionális modellezés alapköveit. A modellezés szempontjából nem a tag fizikai megvalósítására helyezzük a hangsúlyt, hanem az általa megvalósított funkcióra, és ezen belül a rajta keresztül jelek által közvetített információra.

A tagokat a funkcionális modellezésben tipikus grafikus megjelenítéssel ábrázoljuk:

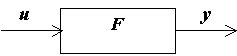
y = F(u)

Az egyszerűség kedvéért a továbbiakban csak a lineáris folytonos rendszerek modellezésével fogunk foglalkozni. Lineárisnak nevezünk akkor egy rendszert, ha abban érvényesül a szuperpozíció elve, azaz elkülöníthető minden egyes bemenetnek a kimenetre gyakorolt hatása. Ez azt is jelenti, hogy egy lineáris tagot (funkcionális modult) első megközelítésben elégséges egy kétpólusú (egy bemenet-egy kimenet) egységként kezelni. Tehát u, y és F skaláris mennyiségek lesznek, vagyis u, y és F.

2.2 Folytonos lineáris rendszerek modellezÉse

2.2.1 Idő-invariáns rendszerek időtartományi modellezése

A dinamikus rendszerek modelljeinek matematikai leírásában az idő mindig a független változó. Egy folytonos, lineáris, idő-invariáns, egy bemenettel és egy kimenettel rendelkező dinamikus rendszer matematikai modelljének általános alakja:

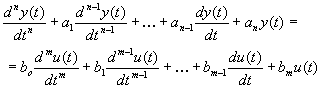(2.2.1)

amely egy nem-homogén lineáris differenciál egyenlet, ahol:

- a rendszer bemenő jele vagy gerjesztő függvénye

- a rendszer kimenő jele vagy válaszfüggvénye

- (), () állandó értékű valós együtthatók (rendszer paraméterek). Valós, fizikai rendszerek esetén (a megvalósíthatóság feltétele). Az együttható, egységnyi értéke miatt nem került kiírásra.

A fenti differenciál egyenlet megoldásának általános alakja:

, (2.2.2)

ahol:

- - a homogén differenciál egyenlet megoldása

- - az inhomogén differenciál egyenlet egy sajátos megoldása

Gyakran az alábbi elnevezéseket is használjuk:

- - az átmeneti (tranziens) válaszfüggvény

- - az állandósult állapot válaszfüggvény

A fenti elnevezéseknek gyakorlati jelentésük van:

- az átmeneti (tranziens) válaszfüggvény nem függ az bemenő jeltől, tehát a magára hagyott rendszer belső struktúráját illetve belső kapcsolatait tükrözi. A szabad válasz elnevezése is használatos.

A valós rendszerekre jellemző az átmeneti (tranziens) viselkedés, mert nem tudják azonnal megváltoztatni az általuk felhalmozott energia szintjét. Ez a felépítésükben fellelhető (mechanikai, villamos, termikus, stb jellegű) tehetetlenségek miatt van, illetve a gyakorlatban nem találunk végtelen értékű energiaforrásokat. Fontos megjegyezzük, hogy a legtöbb valós rendszer tranziens válaszfüggvénye időben nulla fele tart. Ezt a tulajdonságot stabilitásnak nevezzük. A tranziens válasz lefutásának ideje az illető rendszer dinamikájának egy lehetséges mértéke és irányítástechnikai szempontból fontos szereppel bír a beavatkozás gyorsaságának meghatározásánál.

- b) az állandósult állapot válaszfüggvény az inhomogén differenciál egyenlet egy sajátos megoldásán keresztül közvetlenül kapcsolódik az bemenő jelhez, és jellemzi azt az állapotot, amelyet a kimeneti jel (állapotjelző) a bemeneti jel gerjesztő hatására felvesz. A gerjesztett (erőltetett) válasz elnevezése is ismert.

Az állandósult állapot nem jelenti minden esetben azt, hogy az állapotjelzők időben állandó értékeket vesznek fel. Például az irányítástechnikában az állandósult állapot egy adott pontosságnak való megfelelést jelent. Az eltérést hibajelnek nevezik.

2.2.2 Homogén lineáris differenciál egyenletek megoldása

A homogén differenciál egyenletet úgy kapjuk, hogy a (2.2.1) egyenlet jobb oldalát nullával tesszük egyenlővé:

. (2.2.3)

A homogén differenciál egyenlet általános megoldása:

, (2.2.4)

ahol n darab lineárisan független (sajátos) megoldás. Ezek a megoldások egy bázist alkotnak a t független változó valós (vektoriális) terében.

A feladat ennek az n darab lineárisan független megoldásnak a meghatározása.

Az általános (Euler) módszer az (!) behelyettesítéssel elvezet a homogén differenciál egyenlethez kapcsolódó karakterisztikus egyenlethez:

. (2.3.5)

A továbbiakban meg kell határozni a karakterisztikus egyenlet gyökeit. Általában számítógépes segédprogramok, numerikus módszerek segítenek.

A homogén differenciál egyenlet megoldását az alábbi esetek szerint kapjuk meg:

A) A karakterisztikus egyenletnek n darab valós, különböző gyöke van:

A gyököknek megfelelően, az n darab különböző, lineárisan független megoldás van:

(2.3.6)

A homogén differenciál egyenlet megoldása pedig:

, (2.6.7)

ahol n darab integrálási állandó, amelyeket a kezdeti (vagy határ) feltételek értékeiből határozhatjuk meg.

B) A karakterisztikus egyenletnek komplex, de egyszerű gyökei vannak:

Ha a karakterisztikus egyenletnek vannak komplex gyökei is, akkor ezek a konjugáltjukkal párban kell legyenek. Tehát, ha egy egyszerű komplex gyök, akkor komplex konjugáltja is az. Megfelelően, egy komplex gyök párnak két, lineárisan független megoldás felel meg:

. (2.2.8)

A homogén differenciál egyenlet megoldásában a megfelelő rész pedig:

(2.2.9)

C) A karakterisztikus egyenletnek valós többszörös gyökei vannak:

Ha a karakterisztikus egyenletnek egy q-szoros többszörös gyöke, akkor ennek a gyöknek az alábbi q darab lineárisan független megoldás felel meg:

. (2.2.10)

A homogén differenciál egyenlet megoldásában a megfelelő rész pedig:

. (2.2.11)

D) A karakterisztikus egyenletnek komplex többszörös gyökei vannak:

Ebben az esetben a lineárisan független megoldásokat az egyszerű komplex illetve a többszörös valós gyökök eseteinek kombinációjaként kapjuk meg. Tehát, ha például egy komplex kétszeres gyök, akkor szintén kétszeres gyök , azaz annak komplex konjugáltja. A megfelelő lineárisan független megoldások tehát:

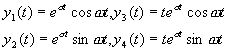, (2.2.12)

míg a homogén differenciál egyenlet megoldásában a megfelelő rész:

. (2.2.13)

Komplex hármas gyökök esetén (amivel már nagyon ritkán találkozhatunk!) két újabb lineárisan független megoldás adódik a meglevőkhöz: és . A gondolatmenetet és a módszert könnyen általánosíthatjuk.

2.2.3 Inhomogén lineáris differenciál egyenletek sajátos megoldása

Az inhomogén lineáris differenciál egyenletek sajátos megoldásának a megtalálása nem mindig egy egyszerű feladat, és bizonyos esetekben kimondottan nehéz illetve számításigényes. Alapvetően az alábbi két módszer ismert:

A) Az ismeretlen együtthatók módszere:

Akkor alkalmazható, ha a (2.2.1) alakú lineáris differenciál egyenlet jobb oldala egy polinom, egy exponenciális, egy szinuszos vagy koszinuszos kifejezés, illetve ezen függvények lineáris kombinációi. A modellezés mérnöki gyakorlatában a bemeneti jeleket a legtöbbször ilyen függvényekkel közelítjük meg (polinom kifejtés, Taylor sor, Fourier sor, stb).

A módszer alapötlete a szuperpozíció elvén alapszik: a sajátos megoldásnak a differenciál egyenlet jobb oldalával azonos alakú (lásd alábbi táblázat), de ismeretlen együtthatókkal rendelkező kifejezés kell legyen.

A szabály a következő:

- ha az egyenlet jobb oldala a táblázat első oszlopában levő függvények összege, akkor alakja a második oszlop megfelelő függvényeinek összege lesz.

- ha az valamelyik tagja a homogén differenciál egyenlet megoldása is, akkor azt a tagot meg kell szorozni t-vel (a független változóval) annyiszor, ahányszor többszörösen szerepel a homogén differenciál egyenlet megoldásában.

- az együtthatókat az így felírt sajátos megoldásnak a differenciál egyenletbe való behelyettesítésével lehet (kell) meghatározni.

1.sz. Táblázat. Az ismeretlen együtthatók módszere

A jobb oldali kifejezés	alakja

B) A komplex módszer:

Mérnöki alkalmazásokban gyakran a gerjesztő jel egy harmonikus (vagy harmonikus összetevőkre bontható, pl. periodikus) jel, azaz a differenciál egyenlet jobb oldala egy egyszerű szinuszos vagy koszinuszos kifejezés. A táblázat szerint ilyenkor a sajátos megoldás alakja , és a további feladat a és meghatározása. A behelyettesítés legtöbbször nehéz számításokhoz vezet. Ezért jobb a komplex módszer alkalmazása, amely a fentiek helyett az Euler képletet használja:

, (2.2.14)

és a sajátos megoldás alakja az alábbi lesz:

(2.2.15)

Behelyettesítés után a és együtthatók a valós és az imaginárius részek azonosításából könnyen meghatározhatók.

2.2.4 Lineáris differenciál egyenletek megoldása Laplace transzformációval

A Laplace transzformáció alkalmazása nagyon elterjedt a mérnöki gyakorlatban. A transzformáció a lineáris differenciál egyenletet egy algebrai egyenletté alakítja át, amelyet így egyszerűbb kezelni. A kezdeti (perem) feltételek eleve a differenciál egyenlet megoldási folyamatába bekerülnek és így a megoldás közvetlenül adódik.

A Laplace módszer szerint a (2.2.1) típusú egyenlet megoldása három fő lépésből áll:

1. A direkt Laplace transzformáció segítségével az adott differenciál egyenletet egy "egyszerű" algebrai egyenletté alakítjuk át.

2. "Egyszerű" algebrai manipulációkkal megoldjuk a kapott algebrai egyenletet.

3. Az inverz Laplace transzformáció segítségével a kapott algebrai megoldásokból meghatározzuk a differenciál egyenlet időtartományi megoldását.

A Laplace transzformáció

Egy adott függvény Laplace transzformációját az alábbi képlettel definiáljuk:

, (2.2.16)

ahol a Laplace transzformáció általunk használt szimbóluma, a Laplace transzformáció változója, vagy más néven a Laplace operátor.

Az függvény (szakaszosan) folytonos és korlátos kell legyen (azaz minden , adott , valós értékekre). A fenti képletet még egyoldalú Laplace transzformációnak is nevezik, mert az integrál határai és között vannak, vagyis a időpont előtti jelben tartalmazott információ elvész. Ez a legtöbb esetben nem jelent gondot, mert az elemzés kezdeti időpontja általában a érték.

2. sz. táblázat. Néhány gyakran használt függvény Laplace transzformáltja

- egység impulzus
- egység ugrás