Az inverz Laplace transzformáció
Az inverz Laplace transzformációt az alábbi képlet szerint definiáljuk:
![]() , (2.2.17)
, (2.2.17)
ahol ![]() -1 az inverz Laplace transzformáció szimbóluma, c pedig az
-1 az inverz Laplace transzformáció szimbóluma, c pedig az ![]() legnagyobb
szinguláris pontját meghatározó komplex érték valós részénél egy nagyobb valós
érték. Szinguláris pont az, amelyre egy komplex függvény nem definiálható.
legnagyobb
szinguláris pontját meghatározó komplex érték valós részénél egy nagyobb valós
érték. Szinguláris pont az, amelyre egy komplex függvény nem definiálható.
A legtöbb mérnöki alkalmazás esetében ritkán használjuk ezeket a képleteket. Annál inkább a transzformációs táblázatokat illetve a transzformáció tulajdonságait.
A Laplace transzformáció fő tulajdonságai
1. Linearitás
![]() . (2.2.18)
. (2.2.18)
2. Valós transzláció
![]() (2.2.19)
(2.2.19)
3. Komplex transzláció
![]() . (2.2.20)
. (2.2.20)
4. A derivált Laplace transzformáltja
![]() . (2.2.21)
. (2.2.21)
Általában
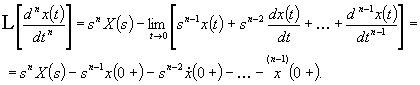 (2.2.22)
(2.2.22)
5. Az integrál Laplace transzformáltja
![]() . (2.2.23)
. (2.2.23)
Általában
![]() . (2.2.24)
. (2.2.24)
6. Skálázás
![]() (2.2.25)
(2.2.25)
7. t-vel való szorzás
![]() . (2.2.26)
. (2.2.26)
Általában
![]() . (2.2.27)
. (2.2.27)
8. t-vel való osztás
![]() . (2.2.28)
. (2.2.28)
A fenti képlet ugyanúgy általánosítható.
9. Konvoluciós integrál
![]() . (2.2.29)
. (2.2.29)
10. Kezdeti érték tétel
![]() . (2.2.30)
. (2.2.30)
11. Végérték tétel
![]() . (2.2.31)
. (2.2.31)
A Laplace transzformáció alkalmazása lineáris
differenciál egyenletek megoldására
A Laplace transzformáció, annak tulajdonságai valamint a transzformációs táblázat segítségével a lineáris differenciál egyenletek megoldása viszonylag könnyű feladat.
Alkalmazva a Laplace transzformációt és a deriválás tételét a (2.2.1) differenciál egyenlet minden egyes tagjára az egyenlet bal oldali tagjainak transzformáltjai:
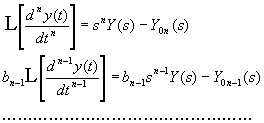 , (2.2.31)
, (2.2.31)
az egyenlet jobb oldali tagjainak transzformáltjai pedig rendre:
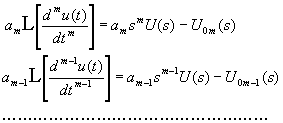 , (2.2.32)
, (2.2.32)
ahol az ![]() (
(![]() ) és
) és ![]() (
(![]() ) polinomok az adott kimenő illetve a bemenő jelek
kezdeti feltételeihez kapcsolódnak.
) polinomok az adott kimenő illetve a bemenő jelek
kezdeti feltételeihez kapcsolódnak.
Összegezve mindent és a kezdeti feltételeket tartalmazó tagokat leválasztva kapjuk:
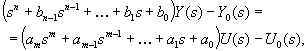 (2.2.33)
(2.2.33)
A fenti egyenletből kifejezzük az ![]() -t, azaz:
-t, azaz:
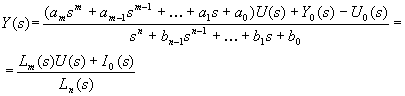 , (2.2.34)
, (2.2.34)
Ahol ![]() a kezdeti
feltételeket összesítő polinom, azaz:
a kezdeti
feltételeket összesítő polinom, azaz:
![]() . (2.2.35)
. (2.2.35)
Ha elemezzük a kapott képleteket, akkor könnyen rájövünk,
hogy az ![]() a karakterisztikus
polinom kifejezésével megegyezik, tehát ugyanúgy a differenciál egyenlet
homogén részéhez kapcsolható.
a karakterisztikus
polinom kifejezésével megegyezik, tehát ugyanúgy a differenciál egyenlet
homogén részéhez kapcsolható.
Nagyon gyakran a mérnöki elemzéseknél a kezdeti feltételeket
meghatározó állapotot referencia állapotnak tekintjük, vagyis a kezdeti
feltételek zérusok, azaz ![]() . Ebben az esetben felírhatjuk:
. Ebben az esetben felírhatjuk:
![]() , (2.2.36)
, (2.2.36)
ahol ![]() az átviteli függvény. Könnyen bizonyítható,
hogy az átviteli függvény a súlyfüggvény
Laplace transzformáltja. A
súlyfüggvény a lineáris, idő-invariáns rendszernek (modellnek) az egységimpulzus bemenő jelre adott
válaszfüggvénye.
az átviteli függvény. Könnyen bizonyítható,
hogy az átviteli függvény a súlyfüggvény
Laplace transzformáltja. A
súlyfüggvény a lineáris, idő-invariáns rendszernek (modellnek) az egységimpulzus bemenő jelre adott
válaszfüggvénye.
Nyomban észrevehető, hogy az ![]() és az
és az![]() polinomokat közvetlenül az eredeti differenciál
egyenletből felírhatjuk. Tehát, az
átviteli függvény minden alapvető információt tartalmaz az adott
rendszerről, tehát alapvető
fogalom számunkra is.
polinomokat közvetlenül az eredeti differenciál
egyenletből felírhatjuk. Tehát, az
átviteli függvény minden alapvető információt tartalmaz az adott
rendszerről, tehát alapvető
fogalom számunkra is.