Az bemenő jel Laplace transzformáltja általában két polinom törtfüggvénye:

, (2.2.37)

ahol az számlálója (numerator) illetve a nevezője (denominator). Behelyettesítve, az számára szintén két polinom törtfüggvényét kapjuk, azaz:

, (2.2.38)

ahol az polinom fokszáma p, a polinom fokszáma q. Az időtartományi választ az inverz Laplace transzformációval kapjuk meg:

. (2.2.39)

Az inverz Laplace transzformáció képletét ritkán használjuk ilyen esetekben, hanem annál inkább a transzformációs táblázatokat. Ehhez viszont a legtöbb esetben a törtfüggvényt előbb résztörtekre kell bontani. Ez utóbbihoz viszont meg kell oldani a egyenletet. Vegyük észre, hogy az egyenletnek p számú gyöke van, ami általában több, mint a karakterisztikus egyenlet gyökeinek száma (). Igaz, a karakterisztikus egyenlet gyökeit (pólusokat) itt is ugyanúgy meg kell határozni. A keresett megoldáshoz az alábbi eseteket különböztetjük meg:

A) Az polinomnak p darab valós, különböző értékű gyöke van:

Az polinomot szorzótényezőkre bontjuk az alábbiak szerint:

, (2.2.40)

ahol az egyenlet gyökei (p darab, különböző érték). A polinom törtfüggvényt rész-törtekként írjuk fel, azaz:

. (2.2.41)

Az i. tagra alkalmazott inverz Laplace transzformáció az alábbit eredményezi:

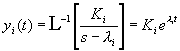, (2.2.42)

Tehát a differenciál egyenlet általános megoldása:

(2.2.43)

lesz, ahol:

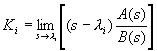, (). (2.2.44)

A kapott megoldás képletéből kitűnik, hogy minden egyen p gyöknek egy típusú exponenciális tag felel meg. Ahhoz, hogy időben csillapodó (amplitúdóban csökkenő) választ kapjunk, az egyes gyökök negatívak kell legyenek (stabilitási kritérium). Egy gyöknek egy állandó érték (a ) felel meg, míg ha valamelyik gyök pozitív, úgy a neki megfelelő válaszfüggvény időben nem csillapodik, azaz a jel amplitúdója növekedik, ami a rendszerben való energia felhalmozásnak a jele. A legtöbb valós rendszerben valamilyen módon ennek korlátozása szokott beállni vagy a felhalmozott energiának köszönhetően a rendszer előbb-utóbb egy strukturális átalakulást fog elszenvedni.

A megoldás képletéből könnyen azonosíthatjuk az homogén (tranziens) és az sajátos (gerjesztett) összetevőket. Ha az karakterisztikus egyenlet n gyöke, akkor a homogén megoldás:

, (2.2.45)

A egyenlet () gyökei adják a sajátos megoldást:

(2.2.46).

Ezek az eredmények csak újból aláhúzzák azt a megállapítást, hogy a homogén megoldás a rendszer belső struktúrájával hozható kapcsolatba, míg a sajátos megoldás az illető rendszer és a környezete közötti kölcsönhatást, a környezetnek a gerjesztő jelen által a rendszerre gyakorolt hatását jellemzi.

B) Az polinomnak valós, de többszörös gyökei (is) vannak:

Feltételezzük, hogy a egy -szoros valós gyök. Ebben az esetben az polinom szorzótényezőkre bontása az alábbiak szerint történik:

. (2.2.47)

A résztörtekre való bontás ebben az esetben az alábbi lesz:

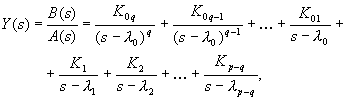(2.2.48)

Az egyszerű gyökök állandóit a (2.2.44) képlet szerint, a többszörös gyöknek megfelelő () állandókat az alábbi képlettel számítjuk ki:

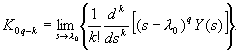(2.2.49)

Az inverz Laplace transzformáció (és a transzformációs táblázat) segítségével az alábbi általános megoldást kapjuk:

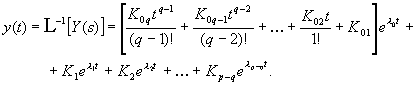(2.2.50)

Látható, hogy a többszörös gyöknek megfelelő minden egyes összetevő tagot beszorozza az exponenciális kifejezés, amely, ha kitevője negatív (), akkor a többszörös gyöknek megfelelő válaszfüggvényt időben teljességében eltünteti.

C) Az polinomnak egyszerű, de komplex gyökei (is) vannak:

A komplex gyökök mindig párban jelennek meg, mert az polinomnak valós együtthatói vannak. A gyökök egymásnak konjugáltjai, azaz ha egy egyszerű komplex gyök, akkor gyök annak konjugáltja is.

Az egyszerű gyökökre érvényes résztörtekre való bontás (2.2.41) képlete ebben az esetben is használható, és az együtthatókat szintén meghatározhatjuk a (2.2.44) képlettel, de a számítások sokkal nehezebbek a komplex számok miatt. Ezért a komplex gyök-párra az alábbiakat írjuk fel:

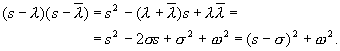(2.2.51)

A megfelelő résztörtre bontás képlete:

. (2.2.52)

A megfelelő inverz Laplace transzformáltat már könnyű meghatározni a táblázatból:

. (2.2.53)

A és együtthatók meghatározása végett előbb kiszámítjuk a komplex értéket:

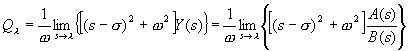, (2.2.54)

amelyből azután azonosítással meghatározzuk a és együtthatókat, mint a komplex érték imaginárius illetve valós részét:

. (2.2.55)

D) Az polinomnak többszörös komplex gyökei (is) vannak:

Az egyszerűség kedvéért feltételezzük, hogy a komplex gyök-pár kétszeres. A résztörtekre bontás során nekik az alábbi kifejezésű megfelelő tagokat kapjuk:

, (2.2.56)

Mivel felírhatjuk, hogy és , a (2.2.52) képlethez hasonló résztörtekre bontást alkalmazhatunk. Ezek szerint:

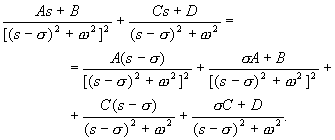(2.2.57)

A megfelelő inverz Laplace transzformáltat könnyű meghatározni a táblázatból:

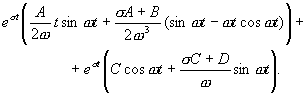(2.2.58)

Az összefüggésben szereplő A, B, C és D együtthatókat az alábbiak szerint határozzuk meg. Előbb kiszámítjuk:

(2.2.59)

majd

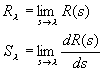, (2.2.60)

Az A, B, C és D együtthatókat az alábbiak szerint azonosítjuk:

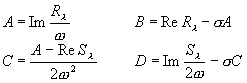(2.2.61)

Mint látható, a számítások elég bonyolultak. Szerencsére az ilyen esetek (kétszeresnél többszörös komplex gyökök) a mérnöki gyakorlatban nagyon ritkán fordulnak elő. Az általánosításra egyébként lehetőség van, de ettől eltekintünk.

2.2.5 Folytonos, lineáris holtidős folyamatok modellezése

Számos valós rendszer esetében a jelfolyamatokban egy jellegzetes időbeni késést, lemaradást vehetünk észre. Ez a jelenség a rendszert alkotó egyes objektumok közötti fizikai szeparációnak illetve az objektumok közötti és az objektumokban történő anyag és/vagy energia áramlás véges sebességének köszönhető. Ezt az időbeni késést holtidőnek (dead-time) nevezzük, megkülönböztetve ezt a fajta késést a rendszerben fellelhető tehetetlenségeknek köszönhető időbeni lemaradásoktól, amelyeket időállandókkal jellemzünk. A holtidő jelenléte szinte valamennyi rendszertípusnál tipikusnak mondható, legyen az hidraulikus, pneumatikus, mechanikus vagy villamos jellegű. "Tiszta" holtidő jellemzi például a szállítószalagokon illetve a vezetékeken (gáz, kőolaj, víz) történő anyagszállítást, de jól érezhetjük ennek hatását a műholdas jeltovábbításban is. A számítógépes véges sebességű és szekvenciális jelfeldolgozás is holtidőt eredményez a jelfolyamatokban.

Matematikailag a holtidő az adott időfüggvény változója értékének eltolásaként fejezhető ki. Egy lineáris, folytonos holtidővel rendelkező rendszermodellt kifejező differenciál egyenlet általános alakja a következő:

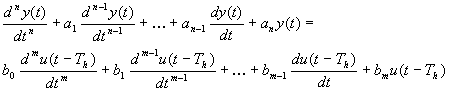(2.2.62)

ahol a holtidőt jelenti. Könnyű észrevenni, hogy egy ilyen modell megoldása semmivel nem jelent többet, mint megoldani azt a holtidő nélkül, majd a kapott időfüggvény a holtidő értékével késleltetni. Mindezt a Laplace transzformáció segítségével az átviteli függvény kifejezésében is egyszerűen kezelhetjük:

(2.2.63)

azaz a holtidős rendszer átviteli függvénye egyenlő a holtidő nélküli rendszer átviteli függvényének és a holtidőt tartalmazó tagnak szorzatával.

Az exponenciális tag jelenléte egyrészt a matematikai kifejezést bonyolítja, másrészt általa a rendszer modelljének foka végtelen lesz (az exponenciális tag csak végtelen Taylor sorba fejthető ki). A mérnöki gyakorlatban az exponenciális tagot polinom megközelítésekkel szokták helyettesíteni. Ezek közül a leggyakoribbak:

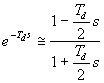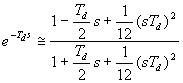, , (2.2.64)

Az első képlet egy elég durva megközelítés. A két utolsó képlet az elsőfokú Padè approximáció illetve a másodfokú Padè approximáció nevet viselik és sokkal jobb megközelítést adnak.