2.3 Folytonos rendszerek modellezése az állapottérben

2.3.1 Alapfogalmak

A valós rendszerek állapottéri leírása (állapot egyenletek) a matematikai modellezés egyik modern alternatívája. Az állapottéri modellezés, általános módszerként, nem csak a lineáris, idő-invariáns rendszerekre alkalmazható, hanem a nemlineáris, időben változó rendszerekre is. A módszer könnyen kiterjeszthető a többváltozós (több bemenettel és több kimenettel rendelkező) rendszerekre, illetve az időben folytonos vagy diszkrét és az eseményvezérelt rendszerekre is.

Egy rendszer állapota alatt a rendszer állapotjelzőinek adott időpillanatban felvett értékeinek halmazát értjük. Matematikai szempontból a rendszer állapotának időbeni jellemzésére (modellezésére) megfelelően megválasztott állapotváltozók és a velük felírható megfelelő állapotegyenletek használatosak.

Legyen az általunk választott állapotváltozók halmaza, mint időfüggvények halmaza. Valamely rendszer állapotváltozói az alábbi két feltételnek kell eleget tegyenek:

1., Bármely kezdeti időpontnak megfelelő értékhalmaz az adott időpontban a rendszer kezdeti állapotát határozza meg.

2., Ha egy rendszer bemenetei időre ismertek és a rendszer kezdeti állapota (az értékhalmaz) specifikált, akkor az állapotváltozók a rendszer jövőbeni () állapotát, azaz az értékhalmazt teljesen és egyértelműen meghatározzák.

Időben folytonos (vagy diszkrét) rendszereknél az állapotegyenletek egyszerű első fokú differenciál (vagy differencia) egyenletek, amelyeket a rendszer állapotváltozói és bemenete(i) közötti összefüggések írják le. Általában ezt felírható úgy mint:

(2.3.1)

ahol az n állapotváltozó, a p bemeneti változó, az i. () állapotleíró relációs függvény és t az idő (független változó).

Ha az adott rendszernek q kimenete van, a kimeneteket szintén kifejezhetjük az állapotváltozók és a bemeneti változók segítségével. Ezek a kimenet egyenletek:

(2.3.2)

ahol a q kimeneti változó, az i. () kimenetet leíró relációs függvény és t az idő (független változó). Az f és g függvényvektorok nemlineárisak és időben változóak is lehetnek, igazolva a módszer általános voltát.

Az állapotegyenletek és a kimeneti egyenletek együtt az állapottéri modellt alkotják.

Vegyük észre, hogy az állapotváltozók nem szükségszerűen a kimeneti változók. Egy rendszer kimeneti változói általában jól meghatározható és mérhető fizikai mennyiségek, míg az állapotváltozók a legtöbbször nem. Az állapotváltozók gyakran általunk csak elméletileg értelmezhető belső rendszerváltozók szerepét töltik be.

Jelöljük vastag kisbetűkkel az alábbi vektorokat:

, állapot vektor (2.3.3)

, bemenet vektor (2.3.4)

, kimenet vektor (2.3.5)

A (2.3.1) állapotegyenleteket az alábbiak szerint vektoriálisan is felírhatjuk:

(2.3.6)

ahol f egy oszlopmátrix (vektorfüggvény), amelynek elemei az függvények. A (2.3.2) kimenet egyenleteket szintén összevonhatjuk:

(2.3.7)

ahol g egy oszlopmátrix, amelynek elemei a függvények.

Tehát, az állapottérben egy időben folytonos rendszer matematikai modellje a:

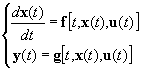(2.3.8)

alakú egyenletrendszer.

Ha mindezt időben diszkrét rendszerekre vetítjük, akkor a matematikai modell alakja:

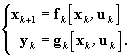(2.3.9)

ahol a k az időbeni szekvenciát jelöli. Mintavételes (időben diszkrét) rendszerek esetében jellemzően a mintavételezési periódusidő állandó. Ilyenkor a k. időpont (szekvencia) a reláció szerint kerül meghatározásra.

2.3.2 Lineáris, idő-invariáns rendszerek modellezése az állapottérben

Az idő-invariáns rendszerek matematikai modelljeiben az idő, mint független változó nem jelenik meg külön (explicit módon), hanem csak a rendszer változóinak leírásában (a rendszer változói időfüggvények). Ha a rendszer lineáris, akkor az állapottéri modellben az és függvények többváltozós lineáris függvények. Ez azt jelenti, hogy kifejezéseik az állapotváltozók és az bemeneti változók lineáris kombinációi.

A lineáris kombináció jelenléte azt is jelenti, hogy az állapotváltozók (és a bemeneti változók is!) lineárisan függetlenek, és mint (normalizált) vektormennyiségek az általuk meghatározott n-dimenziós térben – az állapottérben – egy bázist alkotnak.

A lineáris, idő-invariáns rendszerek matematikai modellje legegyszerűbben mátrixos alakban írható fel az állapottérben:

Állapot egyenlet: , (2.3.10a)

Kimenet egyenlet: , (2.3.10b)

ahol: - A a rendszer mátrix (dimenziója ),

- B a bemenet mátrix (dimenziója ),

- C a kimenet mátrix (dimenziója ),

- D a kimenet-bemenet mátrix (dimenziója ).

Ha rendszerünk csak egy bemenettel és egy kimenettel rendelkezik, akkor a fenti modellegyenletek egyszerűbbek lesznek:

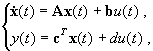(2.3.11)

ahol a B és C mátrixok b () illetve c () vektorokká redukálódnak, míg a D mátrixnak (esetleg) egyetlen d eleme lesz. Fenti jelölésünkben a pont az idő szerinti differenciált helyettesíti, míg a "^T" a transzponálási műveletet jelzi.

2.3.3 A differenciál egyenletek és az állapottér modell közötti kapcsolat

A differenciál egyenletekkel való leírás és az állapottér modell között közvetlen kapcsolat van. Ezt az a matematikai tétel fejezi ki, amely szerint egy n-ed fokú differenciál egyenlet mindig felírható n darab elsőfokú differenciál egyenletből álló egyenletrendszerként, és fordítva. A két leírás tehát ekvivalens, ami azt is jelenti, hogy ugyanannak a rendszernek a matematikai modellje más-más formát is felvehet.

Mint azt később látni fogjuk, egy adott lineáris differenciál egyenletnek végtelen sok módon lehet állapottéri leírást megfeleltetni. Ezek közül a mérnöki gyakorlatban az alábbi módszerek a leginkább használatosak.

A) Az általános programozás módszere

Legyen az adott az alábbi általános alakú n-ed fokú lineáris (állandó együtthatójú) differenciál egyenlet:

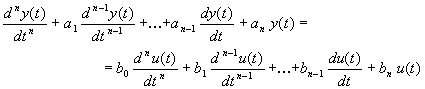(2.3.12)

és definiáljuk az állapotváltozókat az alábbi módon:

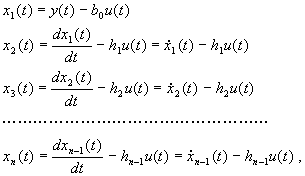(2.3.13)

ahol

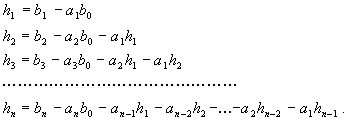(2.3.14)

A fenti jelölésekkel az állapottéri modell már könnyen felírható az alábbiak szerint:

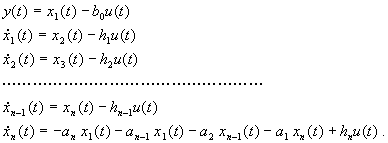(2.3.15)

Az első egyenlet a kimenet egyenlet, míg a következő n egyenlet az állapot egyenlet elsőfokú differenciálegyenleteit határozza meg. A (2.3.11) egyenlet jelölései szerint:

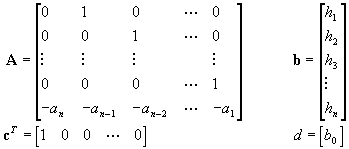(2.3.16)

Jól látható, hogy az általános programozás módszere könnyen algoritmizálható és egyszerűen implementálható egy számítógép programjaként.

Vegyük észre, hogy az A rendszer-mátrix elemei a homogén differenciál egyenlet együtthatói, vagyis az A rendszer-mátrix a rendszer belső struktúráját (viselkedését) foglalja magába. A b bemenet-mátrix (vektor) a bemeneti jel és az állapotváltozók közötti kapcsolatot teremti meg, míg a c kimenet-mátrix (vektor) az állapotváltozók és a kimeneti jel közötti kapcsolatot írja le. A bemeneti jel és a kimeneti jel közötti közvetlen kapcsolatot a bemenet-kimenet mátrix egyetlen d eleme végzi. A legtöbb valós rendszer esetén ez a kapcsolat (mátrix) nem létezik, pontosabban .

B) A közvetlen programozás módszere

Legyen adott ugyanaz a (2.3.12) n-ed fokú lineáris differenciál egyenlet, amelyben írjuk át a differenciálás műveletét a D differenciáló operátorral az alábbiak szerint:

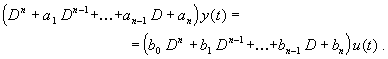(2.3.17)

Jelöljük a továbbiakban:

(2.3.18)

A fenti két egyenletből könnyen felírhatjuk azt, hogy:

(2.3.19)

A kapott egyenlet alakját tekintve, azonos a (2.3.12) differenciál egyenletével, azzal a különbséggel, hogy nem szerepelnek benne a bemeneti jel felsőbb deriváltjai. Az függvény csak a közbenső számolásokhoz szükséges segédváltozó jelölés.

Ha a (2.3.19) differenciál egyenlet számára az állapotváltozókat fázisváltozóknak választjuk, azaz az állapotváltozók a kimenet és annak deriváltjai, akkor felírhatjuk:

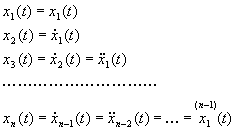(2.3.20)

majd a (2.3.18) és (2.3.19) egyenletek segítségével az alábbiakat kapjuk:

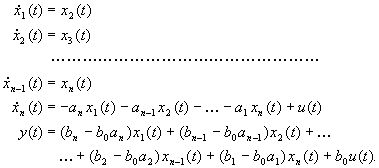(2.3.21)

Az állapottéri modellt leíró mátrixok az alábbiak lesznek:

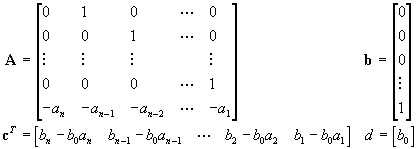(2.3.22)

A közvetlen programozás módszere a legegyszerűbben alkalmazhatók közé tartozik. Nem csak könnyen algoritmizálható, hanem vegyük észre milyen könnyen felírható az A rendszermátrix illetve a b vektor. Valós rendszermodellek esetén a c vektor elemei közül is általában nagyon sok a zérus (mert a bemenő jel magasabb rendű deriváltjai hiányoznak) és általában is igaz.

A közvetlen programozás módszerével meghatározott állapottéri modellt kanonikus fázisváltozós alaknak is nevezik.

C) A párhuzamos programozás módszere

Legyen adott ugyanaz a (2.3.12) n-ed fokú lineáris differenciál egyenlet, amelyet írjuk át az alábbiak szerint:

. (2.3.23)

Ha az nevező polinomnak a egyszerű és valós gyökei vannak, akkor a polinomot felírhatjuk szorzótényezős alakban, mint:

, (2.3.24)

A (2.3.23) összefüggésben a polinomiális törtet egyszerű résztörtekre bontjuk, azaz:

(2.3.25)

Az összeg i. tagjának az alábbi elsőfokú differenciál egyenlet felel meg:

. (2.3.26)

Ezek után már könnyű meghatározni az állapottéri modellt leíró mátrixokat:

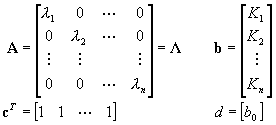(2.3.27a)

vagy

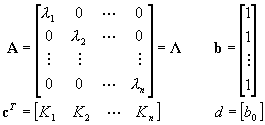(2.3.27b)

A párhuzamos programozás módszerével meghatározott állapottér modellt kanonikus alaknak nevezik.

A párhuzamos programozás módszere a legegyszerűbb matematikai kifejezési formát adja, mert egymástól függetlenül megoldható elsőfokú differenciál egyenletekhez vezet. (Ez azt is jelenti, hogy az így meghatározott állapotváltozók teljesen - nem csak lineárisan!- függetlenek egymástól, azaz az állapotteret kifeszítő állapotváltozók - bázisvektorok - merőlegesek egymásra. A legtöbb valós rendszer (modell) esetében mindez (sajnos) nem áll fenn, és modellezési célokra az állapottéri modell további transzformációkat igényel.

A módszer hátránya, hogy meg kell oldani ugyanazt az karakterisztikus egyenletet. Könnyen bizonyítható viszont, hogy a karakterisztikus egyenlet gyökei az A rendszer-mátrix sajátértékei. Szintén nehézséget jelent az, hogy többszörös és esetleg komplex gyökök esetén a kanonikus alak felírása már sokkal bonyolultabb. A feladat az A rendszer-mátrix (kvázi) átlós felírásában merül ki, amelyet az A mátrix ún. Jordan kanonikus alakjának meghatározása jelenti.

D) A soros programozás módszere

Legyen adott ugyanaz a (2.3.12) n-ed fokú lineáris differenciál egyenlet. A soros programozás módszere az állapottéri modell alábbi mátrixaihoz vezet:

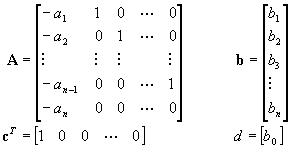(2.3.28)

A soros programozás módszere a lehető legegyszerűbben vezet az állapottér modellhez. A bizonyítást az olvasóra bízzuk.

A soros programozás módszerével meghatározott állapottér modellt kanonikus fizikai alaknak nevezik.

E) Az állapottér modell lineáris transzformációja

Láttuk, hogy egy differenciál egyenletnek többféle megfeleltetése is van az állapottérben. Azt is megjegyeztük, hogy a normalizált állapotváltozók az állapottér egy bázisát határozzák meg. A lineáris algebra elméletéből tudjuk, hogy egy n dimenziós vektoriális térben bázist tudunk váltani egy T transzformációs mátrix segítségével. Az egyedüli megkötés csak az, hogy a transzformációs mátrix reguláris kell legyen, ami azt is jelenti, hogy elméletileg végtelen módon végezhetünk ilyen transzformációt, illetve azt is, hogy az állapotváltozókat végtelen féle (pontosabban a nekünk legmegfelelőbb!) módon választhatjuk és használhatjuk fel. A dolog viszont (sajnos) mégsem jelent mindig előnyt, mert adott lineáris transzformációval az állapotváltozók fizikai jelentését is elveszíthetjük. Ez nem is annyira a modellezés, mint az irányítás szempontjából esetleg komoly gondot jelenthet.