A lineáris transzformáció nem változtatja meg az állapottér modell alakját. Bizonyításként jelölje  az új állapotvektort, azaz:

,                                                                         (2.3.29)

ahonnan következik, hogy:

.                                                                       (2.3.30)

Behelyettesítve a (2.3.11) egyenleteibe, következik:

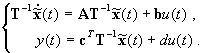                                                  (2.3.31)

Ha az első egyenletet balról beszorzunk T–vel és az alábbi jelöléseket :

,                                   (2.3.32)

eszközöljük, akkor az alábbi új állapottér leírást kapjuk:

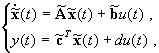                                                           (2.3.33)

amely alakjában a (2.3.11) egyenletekhez teljesen megfelel.

Mindebből levonható az a következtetés, hogy a (2.3.11) egyenletek az állapottérben egy általános modell leírást jelentenek (lineáris, egyváltozós rendszerek esetére). A lineáris transzformáció nem változtatja meg a modell alakját (sem a karakterisztikus egyenlet, sem a sajátértékek nem változnak), csak esetleg annak leírásában szereplő mátrixainak elemeit A gyakorlatilag végtelen állapottéri leírás lehetősége közül a probléma mindig megtalálni az adott alkalmazás számára a legmegfelelőbbet.

2.3.4 Lineáris, idő-invariáns állapottér modellek megoldása

A)   A szabad válasz meghatározása

Induljunk ki az állapottér modell kanonikus alakjából és az egyszerűség kedvéért feltételezzük, hogy a rendszer-mátrix sajátértékei egyszerűek és valósak. Ilyenkor az állapottér modell (2.3.26) alakú, független elsőfokú differenciál egyenletekből áll. Egy ilyen differenciál egyenlet szabad válasza (homogén részének megoldása):

                                                                      (2.3.34)

alakú. Ha minden egyes differenciál egyenlet szabad válaszát felírjuk, akkor az állapottérben a szabad válasz alábbi mátrixos alakban írható fel:

                                    (2.3.35)

Jelölje továbbiakban az exponenciális függvényeket tartalmazó mátrixot , azaz:

                                                                    (2.3.36)

A  mátrixot modál átmeneti mátrixnak nevezzük, mert az egymástól független állapotváltozókat modál változóknak is szokták nevezni. A modál változók írják le azt a módot, ahogyan az állapottér adott, egymástól független koordinátái mentén az időbeni változások végbemennek, azaz ahogyan a változásokat az egyes elsőfokú differenciál egyenletek skaláris megoldása azt mutatja. Könnyen bizonyítható, hogy:

                                                                          (2.3.37)

ahol a  mátrix a sajátértékek átlós mátrixa. Tudjuk már, hogy az állapotér-modell kanonikus alakjánál a rendszer-mátrix átlós alakú, és hogy az átlón a rendszer-mátrix saját értékei szerepelnek. A lineáris algebrából szintén tudjuk, hogy bármely (négyzetes) mátrix átlós alakját egy megfelelően elvégzett lineáris transzformáció segítségével is meghatározhatjuk. A transzformációs mátrixot modál mátrixnak nevezzük. Jelöljük ezt M–el, és alkalmazzuk ezt a transzformációt a (2.3.36) egyenletre, azaz

                                                      (2.3.37)

vagy

                                                           (2.3.38)

Ezekkel a behelyettesítésekkel nem csináltunk mást mint meghatároztuk az állapottér-modell egy általános alakjának a szabad válaszát. Ugyanis, ha

                                                                (2.3.39)

jelöli az állapot átmeneti mátrixot, akkor könnyen bizonyítható, hogy:

                            (2.3.40)

A (2.3.38) egyenletet, mint az állapottér-modell szabad válaszát felírhatjuk mint:

                                                          (2.3.41)

amelynek alakja hasonlít egy elsőfokú rendszer szabad válaszához (csak mátrixos-vektoriális felírású). Ha az A rendszer-mátrix dimenziója , akkor a  állapot átmeneti mátrix dimenziója is . Látható, hogy a  állapot átmeneti mátrix az x(0) kezdeti állapotra hat, meghatározva a rendszer állapotát bármelyik t időpontban.

Az állapot átmeneti mátrix tulajdonságai jelentős számítási előnyökhöz vezetnek:

                                                                       (2.3.42a)

                                           (2.3.42b)

                                                    (2.3.42c)

                 (2.3.42d)

               (2.3.42e)

Az állapot átmeneti mátrix meghatározása

Láttuk, hogy az állapottér modell megoldásához meg kell határozni a  állapot átmeneti mátrixot, és ez nem mindig könnyű feladat. Fennebb láttuk, hogy ennek egyik módja az, hogy előbb Jordan kanonikus (átlós) alakra hozzuk az A rendszer-mátrixot, majd az M modál transzformációs mátrix segítségével meghatározzuk a  állapot átmeneti mátrixot. A módszer azonban ritkán praktikus, egyfelől, mert meg kell tudni határozni a saját értékeket, azaz meg kell tudni oldani egy n-ed fokú polinom egyenletet, másfelől meg kell határozni a modál mátrixot, azaz meg kell oldani egy  dimenziós lineáris egyenletrendszert. A módszer csak további bonyolultsággal szolgál, ha a sajátértékek nem valósak, illetve ha többszörösek is.

A Laplace transzformáció módszere egy alternatív, bizonyos esetekben egyszerűbb megoldási módszer. Ha  a Laplace transzformációt alkalmazzuk a homogén állapot egyenletre, következik:

                                                               (2.3.43)

ahonnan:

                                                               (2.3.44)

A szabad választ az inverz Laplace transzformációval határozzuk meg

                                                         (2.3.45)

Azonosítva a kapott eredményt a (2.3.41) egyenlettel, következik, hogy a  állapot átmeneti mátrix meghatározási módja:

                                                              (2.3.46)

Bár a képlet most is egyszerű, a megoldás mégis gondokkal jár. Egyrészről itt is szükségünk van a karakterisztikus egyenlet megoldásaira, másrészről a modál mátrix meghatározása helyett most, az s változó miatt egy szimbolikus mátrix inverziót kell megvalósítanunk, amely magasabb rendű rendszerek esetén nehézséget jelenthet.

A gyakorlatban, főleg számítógépes megvalósításoknál, ahol amúgy is a megoldásnak csak bizonyos időközönkénti értékeire van szükségünk, sokszor megelégszünk egy megközelítő megoldással. Egy ilyen megközelítő megoldás a  állapot átmeneti mátrix Taylor-polinom sorba való bontása, az alábbiak szerint:

                                   (2.3.47)

A polinom sorba bontás előnye, hogy az algoritmus ciklusa az A rendszer-mátrix sorozatos szorzatát számítja. A pontosságot a sorban levő tagok száma határozza meg, amit általában a rendelkezésre álló számítási idő határoz meg. Ha egy állandó T mintavételezési periódusidővel dolgozunk, akkor elégséges a  értékét egyszer meghatározni, majd a további időpontokra alkalmazni az állapot átmeneti mátrix (2.3.42c) tulajdonságát. Ez nagyságrendileg csökkenti a számítási igényeket.

B)   A gerjesztett válasz illetve az általános megoldás meghatározása

Induljunk ki a lineáris állapottér modell állapotegyenletének általános alakjából:

 ,                                                              (2.3.48)

amelyet átírunk az alábbi alakra:

 .                                                              (2.3.49)

Ez utóbbi egyenlet mindkét oldalát beszorozzuk az  taggal, és kapjuk:

.                                 (2.3.50)

Ha a fenti egyenlet mindkét oldalát integráljuk 0 és t határértékek között, akkor:

.                                                 (2.3.51)

Ha most még egyszer az egyenlet mindkét oldalát beszorozzuk az  taggal, az:

                                               (2.3.52)

egyenletet kapjuk. Tudva azt, hogy , valamint azt, hogy , a behelyettesítések alábbi általános megoldáshoz vezetnek:

.                                        (2.3.53)

Az általános megoldásból könnyen azonosíthatjuk a szabad választ (az első tagot) valamint a gerjesztett (erőltetett) választ (az összeg második tagját).

Ha a kezdeti időpont t0 és nem t = 0, akkor az általános megoldás képlete:

,                                     (2.3.54)

amelyet egy egyszerű időeltolással kapunk meg. Természetesen itt is a megoldás két összetevője ugyanolyan könnyen azonosítható.

Az általános megoldást, illetve annak két összetevőjét a Laplace transzformáció segítségével is meghatározhatjuk. Ha alkalmazzuk a Laplace transzformációt a (2.3.48) állapotegyenletre, akkor az alábbiakat kapjuk:

.                                                   (2.3.55)

ahonnan

 ,                                                    (2.3.56)

illetve

.                                     (2.3.57)

Az általános megoldást az inverz Laplace transzformáció segítségével kapjuk meg:

                       (2.3.58)

A (2.3.45) egyenlet alapján azonosítva a fenti általános megoldásból a szabad választ, a gerjesztett válasz kifejezésére az alábbi összefüggést kapjuk:

.                              (2.3.59)

Természetesen, a Laplace transzformációs módszer itt is ugyanazokat a nehézségeket rejti magába, mint a szabad válasz meghatározása esetén

 

A fennebb bemutatott módszerek lineáris, egy-változós rendszerek állapottéri modell leírásaira, megoldására vonatkoztak. A módszer könnyen kiterjeszthető többváltozós (több bemenettel és több kimenettel rendelkező) állapottéri rendszermodellekre is. Az állapot átmeneti mátrix módszere időben diszkrét állapottéri leírásokra is könnyen kiterjeszthető, és előnye a számítógépes implementáció könnyedségében rejlik. Számos számítógépes szoftvertermék támogatja az ilyen modelleket.

Nemlineáris állapottér modellek esetén a megoldási módszer már nem ilyen könnyű és egyértelmű. Az ilyen esetekben az analitikus megoldás megtalálása nagyon nehéz, általános megoldási módszer pedig nincs. Ezért a numerikus integráló algoritmusok használata preferált, illetve a számítógépes szimulációk elvégzése sokban segíthet. Sajnos, a legtöbb esetben az algoritmusokat maga a felhasználó kell megfogalmazza, illetve a felhasználó kell maga a programokat is megírja.